Фотометрический парадокс Ольберса
Парадокс Ольберса - имеет ли вселенная конец или все-таки бесконечна?
В середине 19-го века астрономия уже давно имеющая в арсенале метод горизонтального параллакса, могла достаточно точно установить расстояния до некоторых ближайших звезд. И это знание несколько обескураживало — получалось, что даже самые близкие из звезд находятся от нашей Солнечной системы на совершенно невероятных расстояниях.

Млечный путь — если смотреть невооруженным взглядом, сплошное «молочное» пятно, а если в телескоп — сплошной сонм звезд.
Существует ли край вселенной и самая далекая звезда?
Но если так далеки близкие звезды, как же тогда далеки дальние? А самые-самые дальние? Земля имеет поверхность конечных размеров, и размеры пространства, занимаемого солнечной системой, тоже конечны. Остаемся ли мы в пределах конечного, поднявшись на ещё одну, новую ступень? Или мы все таки оказываемся лицом к лицу с бесконечностью вселенной — с тем понятием, которое так смущало ученых с самого начала?
Вопросы эти не находят ответа и сейчас, что, в прочем, не мешает нам вновь и вновь ими задаваться.
По-началу всё просто, к примеру, если мы ограничимся лишь той частью Вселенной, которую можно увидеть невооруженным глазом, то такая Вселенная, безусловно, будет конечной. Теперь известно, что по крайней мере в ближайшей к нам области среднее расстояние между звездами составляет примерно 10 световых лет.
Мы знаем также, что невооруженным глазом можно увидеть около 6000 звезд. Предположим, что это — все существующие звезды (то есть вся вселенная!) и что все они находятся друг от друга на указанном выше среднем расстоянии. В таком случае все 6000 звезд уместятся в сфере диаметром примерно 100 парсек, или 330 световых лет.
Это, конечно, достаточно много по обычным человеческим представлениям. Сфера в 100 парсек имеет диаметр примерно в 3 квадрильона, т.д. 3 000 000 000 000 000 км, и ее размеры потрясли бы и ошеломили бы любого астронома, жившего до 1600 г., и многих из живших позже.
Однако эти 6000 звезд — отнюдь не все существующие звезды. Едва Галилео Галилей в 1609 г. навел на небо свой первый телескоп, как обнаружил множество слабых звезд, невидимых невооруженным глазом. И каждое новое усовершенствование телескопа приносило новый обильный урожай еще более многочисленных и еще более слабых звезд.
Сперва не было видно конца этим открытиям, и в 1800 г. вместо Вселенной с диаметром в 100 парсек, включающей 6000 звезд, легко было бы признать существование Вселенной с бесконечным числом звезд и без какого-либо конца в пространстве. В этом случае вопрос: «Как далека от нас самая далекая звезда?», не имел бы смысла, потому что на него можно было бы ответить «Самой далекой звезды не существует!»

Астрономом Генрих Вильгельм Матеус Ольберс — в шутку доказал, что вселенная имеет конец. А разоблачить эту шутку не могут до сих пор!
Суть парадокса Ольберса
Однако мысль о бесконечности, как всегда, была для человечества непереносима. На возможность существования бесконечной звездной Вселенной было начато наступление с двух сторон — и в теории, и в наблюдениях.
Теоретические основания для сомнений в бесконечности звездной Вселенной были сформулированы немецким астрономом Генрихом Вильгельмом Матеусом Ольберсом (1758—1840).
В 1826 г. он пришел к так называемому «парадоксу Ольберса». Чтобы изложить его, начнем с установления следующих предпосылок:
- Протяженность Вселенной бесконечна
- Число звезд бесконечно, и они распределены по Вселенной равномерно.
- Все звезды Вселенной имеют в среднем одинаковую светимость.
Представим себе нашу Солнечную систему в центре подобной бесконечной Вселенной и разделим в своем воображении Вселенную на тонкие концентрические слои, вроде тех, из которых слагается луковица.
Объем каждого из этих тонких слоев будет возрастать пропорционально квадрату расстояния слоя от центра. Если слой А находится в 3 раза дальше от нас, чем слои В, то объем слоя А будет в 32, т.е. в 9 раз больше, чем объем слоя В. И если звезды равномерно распределены по всем слоям (предпосылка 2, см. выше), то слой А, объем которого в 9 раз больше объема слоя В будет содержать и в 9 раз больше звезд.
С другой стороны, свет отдельных звезд ослабевает пропорционально квадрату расстояния до них.
Если слои А в три раза дальше, чем слой В, и содержит в 9 раз больше звезд, то яркость каждой отдельной звезды (при одинаковой средней светимости — предпосылка 3 см. выше) слоя А будет равна (1/3)2, т.д. 1/9 яркости отдельной звезды слоя В.
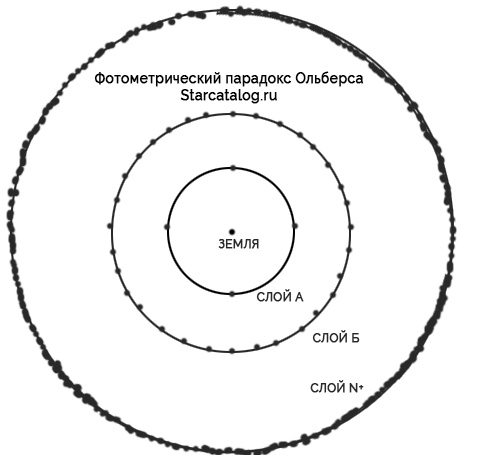
Иллюстрация парадокса Ольберса — представим землю в центре вселенной, а звезды вокруг неё — равномерно размещенными «слоями» по степени удаленности от центра
Таким образом, получается, что слой А содержит в 9 раз больше звезд, чем слой В, и что яркость каждой звезды слоя А равна лишь 1/9 яркости каждой звезды слоя В. Следовательно, общая сумма света, получаемого солнечной системой от слоя А, равна 9×1/9 света получаемого от слоя В.
Иначе говоря, солнечная система получает и от слоя А, и от слоя В равное количество света.
Точно такой же вывод получается для любого другою слоя. Отсюда следует, что если бы количество слоев было бесконечно (предпосылка 1, см. выше), то количество достигающего нас света также было бы бесконечным — при условии, что ближние звезды не заслоняли бы более отдаленных. Но даже если учесть, что ближние звезды заслоняют дальние, все небо должно было бы сиять, как поверхность одного гигантского яркого солнца. А на самом деле этого, разумеется, нет.
Ольберс предположил, что объяснить этот парадокс можно было бы присутствием в космосе пылевых облаков, которые поглощают свет более далеких звезд, так что до нас доходит лишь свет относительно близких звезд. Однако такое объяснение невозможно.
Если бы пылевые облака поглощали свет, они постепенно нагревались бы, пока сами не начали бы испускать столько же света, сколько поглощают. Количество света, достигающего нас, по-прежнему осталось бы бесконечным!
Следовательно, исходные предпосылки Ольберса должны были содержать какую-то ошибку: либо протяженность Вселенной не могла быть бесконечной, либо, если она бесконечна, не могло быть бесконечным число звезд.
Вместо этого следовало предполагать существование конечного (хотя и очень большого) числа звезд, распределенных по конечному (хотя и очень обширному) пространству.


 Навигация
Навигация