Простое объяснение появления черных дыр во вселенной

Можно ли замедлить скорость света - Белые карлики, нейтронные звезды и общая теория относительности - Что такое сингулярность - «Звезда будет бесконечно сжиматься!» - «Черные дыры» или «застывшие звезды»

XIX век – век торжества науки. Ученые уже не “догадывались” как в прошлые столетия, а, накопив солидный багаж знаний, “предсказывали”. Простой пример: Урбен Жан Жозеф Леверье не искал на звездном небе Нептун с помощью телескопа, он  взял и рассчитал его орбиту исходя из данных наблюдений соседних планет и ньютоновской теории гравитации.

Можно ли замедлить скорость света?

И все же, вопросы оставались. Дело в том, что орбиты движения планет все же чуть-чуть отличались от рассчитанных по законам Ньютона и Кеплера. А у Меркурия, положение перигелия отклонялось от предвычисленного на целые 43 угловые секунды в столетие!

Так что когда Альберт Эйнштейн создал частную теорию относительности и занялся теорией тяготения, это не было какой-то прихотью. Просто вопрос уже назрел и на него требовался ответ.

Вскоре Эйнштейн доказал, что перигелий Меркурия должен перемещаться именно на 43 угловые секунды в столетие. Кроме того, из общей теории относительности следовало, что луч света, который прежде считался движущимся только прямолинейно, должен отклоняться от своей прямой траектории, оказавшись в поле тяжести какого-то массивного тела.

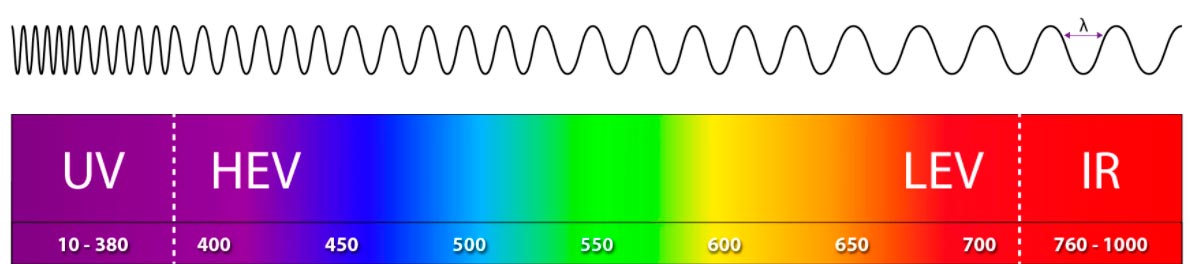
Скорость света не может быть замедлена, но мы можем судить о «замедлении» фотона по падению частоты и как следствие – «покраснению» спектра

Иначе и быть не могло, ведь фотон, квант света – вполне материальная частица, он также как и другие материальные тела должен подчинятся закону тяготения. Никто ещё не знал, чему равна масса фотона, но физики уже знали, как измерить энергию фотона. Из принципа эквивалентности следовало, что и энергия тела эквивалентна вполне определенной массе-вспомните знаменитую формулу Е=МС²!

И значит, луч света должен, как обыкновенный камень, двигаться в поле тяжести по кривой линии, которую можно рассчитать.

Ещё интереснее был другой вопрос: если подбросить вверх камень, то он будет лететь все медленнее, его кинетическая энергия будет расходоваться на преодоление пут тяготения. В конце концов она истратится вся, камень на мгновение остановится и начнет падать. Но ведь и луч света испущенный вверх, против поля тяжести, тоже должен терять свою энергию.

Однако получался парадокс – фотон, то есть частица света, не может двигаться со скоростью отличной от скорости света, ведь скорость света – величина постоянная! Оказалось, что фотон ведет себя иначе. В отличие от камня он теряет энергию по другому – фотон “краснеет”.

Согласно теории квантов (тоже созданной Эйнштейном в 1905 году), энергия фотона пропорциональна его частоте. Меньше энергия – меньше частота. Частота фотона – это его цвет. Значит, цвет луча света меняется. Из голубого луч становится красным, причем тем больше, чем более сильное поле тяжести ему приходится преодолевать. Этот эффект называется гравитационным красным смещением.

Белые карлики, нейтронные звезды и общая теория относительности

В 1919 году Артур Стэнли Эддингтон, наблюдая солнечное затмение, обнаружил, что звезды около затемненного Луной края солнечного диска сместились со своих мест. Это означало, что луч света от далекой звезды, проходя по пути к Земле рядом с Солнцем, отклонялся от прямолинейной траектории. Измеренный эффект смещения практически точно совпал с предсказанным.

А пять лет спустя тот же Эддингтон объявил о том, что спектральные линии элементов в спектрах белых карликов должны быть смещены в красную сторону. Ведь белые карлики – самые компактные из звезд. Поле тяжести на их поверхности в миллион раз больше, чем на поверхности Земли! Значит, и красное смещение света, испущенного белым карликом, должно быть самым большим из возможных.

Эддингтон вычислил, на сколько именно должны смещаться в красную сторону спектральные линии. В том же 1924 году Уолтер Адамс наблюдал спектры белого карлика Сириус В и обнаружил предсказанное красное смещение – именно такое, какое следовало из теории.

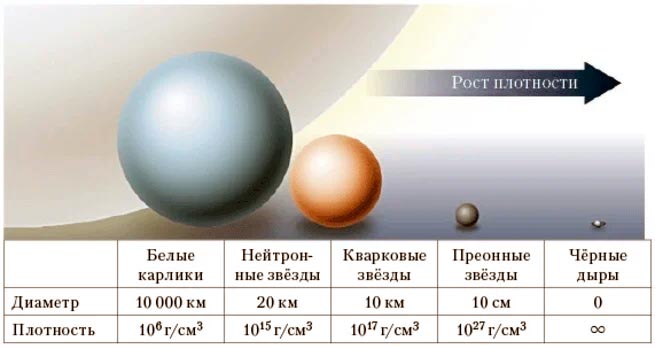
Примерная плотность различных сверхмассивных космический тел: белых карликов, нейтронных, кварковых звезд и т.п.

Размер белого карлика составляет 10 тысяч километров, и в нем уже проявляются эффекты общей теории относительности. Оказывается, без них нельзя точно рассчитать ни предельную массу белого карлика, ни смещение линий в его спектре. Что же тогда говорить о нейтронной звезде, размер которой, если верить предсказаниям Цвикки, еще в сотни раз меньше! Ведь и поле тяжести на поверхности нейтронной звезды должно быть в сотни раз больше!

Чем ближе скорость движения тела к скорости света, тем больше влияние эффектов теории относительности. Характеристикой величины поля тяжести может служить вторая космическая скорость (“скорость убегания”). Чем больше сила тяжести, тем большую скорость должно иметь тело, чтобы улететь в космос.

Чтобы навсегда покинуть Землю, нужно разогнаться до 11 км/с. Чтобы улететь с поверхности Солнца, нужно развить скорость 600 км/с. Чтобы разорвать путы тяжести белого карлика, нужна скорость 5 тысяч км/с. Все больше и больше! Заметьте, что в белом карлике эффекты общей теории относительности уже ощутимы. А чтобы покинуть нейтронную звезду, нужно разогнаться до скорости 100 тысяч км/c. Всего втрое меньше скорости света. Если бы размер нейтронной звезды был втрое меньше, то скорость убегания с ее поверхности сравнялась бы со скоростью света. Улететь с поверхности нейтронной звезды стало бы просто невозможно…

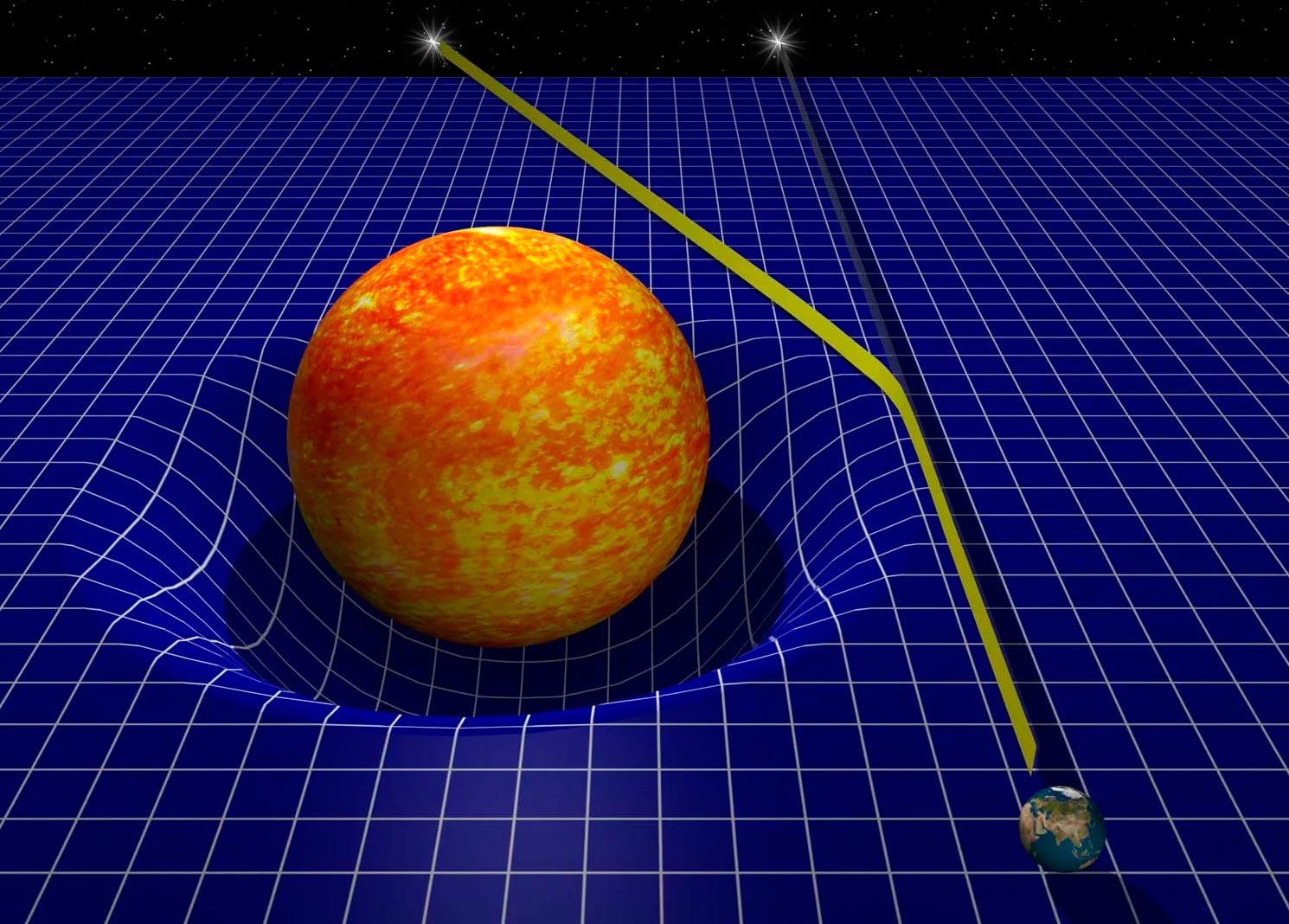
Гравитация массивного объекта отклоняет фотоны света и по этому отклонению, мы можем судить о массе объекта

Впрочем, последнее рассуждение не имеет отношения к нейтронным звездам. Нейтронная звезда в принципе не может иметь таких маленьких размеров – позднее мы еще вернемся к этому. Но само рассуждение безупречно и пришло а голову английскому физику Дж. Мичеллу еще в XVIII веке. Спустя несколько лет после Мичелла о том же писал и великий Лаплас.

Эйнштейн завершил разработку своей теории гравитации в 1916 году. Он создал такие уравнения полей тяжести, которые сводились к обычному ньютоновскому закону всемирного тяготения, если поля слабы. Но что значит – слабы или сильны? Это лишь слова, а чтобы придать им физический смысл, нужно описать их каким-то числом. Скажем, так: если поле тяжести больше некоторого “икс”,, то оно считается сильным, а если меньше – то слабым. Таким пробным камнем для теории тяготения и стала проблема поля тяготения звезды.

Что такое сингулярность

В 1916 году немецкий астроном Карл Шварцшильд, прочитав только что опубликованную работу Эйнштейна, решил так преобразовать уравнения общей теории относительности, чтобы с их помощью можно было бы описать гравитационное поле звезды, то есть поле тяжести вне некоторого сферического тела. Лишь бы только это тело не вращалось. Шварцшильд получил выражение для той критической величины, вблизи которой поле тяжести можно назвать сверхсильным.

Случайно математическое выражение этой величины оказалось в точности таким, какое получил Лаплас для радиуса своей гипотетической невидимой звезды. И тогда выяснилась странная вещь. В уравнении оказалась, как говорят математики, сингулярность. То есть область, в которой поле тяжести обращается в бесконечность.

В обычной ньютоновской формуле закона всемирного тяготения тоже есть сингулярность. Если расстояние между двумя телами равно нулю, то и в ньютоновской теории сила притяжения таких тел друг к другу равна бесконечности. Но эта сингулярность никому не мешает – в природе не может реализоваться случай, когда расстояние между телами точно равно нулю!

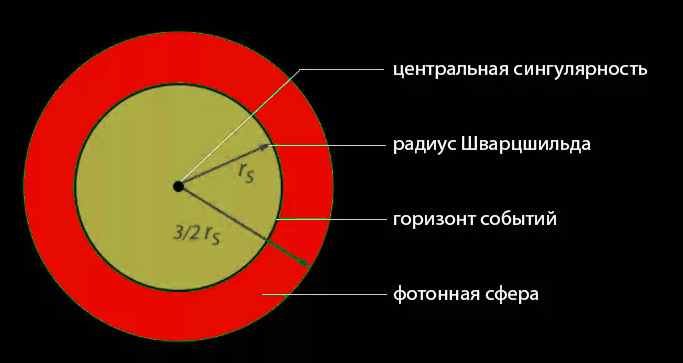
А Шварцшильд в рамках общей теории относительности нашел, что сила тяжести становится бесконечно большой при конечном, не равном нулю, расстоянии. Достаточно сжать звезду до некоторого критического размера, и сила тяжести на поверхности такой звезды станет бесконечно большой. Этот критический радиус и был назван гравитационным радиусом, или радиусом Шварцшильда.

Гравитационный радиус – та граница, с приближением к которой эффекты общей теории относительности неограниченно нарастают.

Переменной величиной в формуле радиуса Шварцшильда является только масса звезды. Чем больше масса звезды, тем больше ее гравитационный радиус. Гравитационный радиус Солнца равен 3 км. Запомните эту цифру – достаточно знать массу звезды, выраженную в массах Солнца, и мы, умножив массу на три, получим величину гравитационного радиуса звезды в км.

Так вот, если радиус звезды ненамного больше гравитационного, то поле тяжести сверхсильно.

Радиус Солнца больше гравитационного в 200 тысяч раз, и эффекты общей теории относительности очень малы, поле тяжести Солнца хорошо описывается ньютоновской теорией (эффекты малы, но все же измеримы – ведь измерено же отклонение луча света в поле тяготения Солнца!).

А вот радиус нейтронной звезды всего 10 км-в 2-3 раза больше гравитационного. Сила тяжести очень велика, без общей теории относительности не обойтись. Какова же этв плотность? Её не сложно рассчитать: сожмем в воображении Солнце до размеров его гравитационного радиуса – 3 км. Разделим массу Солнца, на объем шара радиусом 3 км и получим, что плотность такого шара равна 2 x 10¹⁶ г/см³. Если сказать проще: 20 миллиардов тонн в 1 кубическом сантиметре.

Очень много, невероятно много… но не бесконечно много! А сила тяжести на поверхности такой звезды именно бесконечна. И значит, никакое газовое давление в принципе не удержит в равновесии звезду, радиус которой равен радиусу Шварцшильда. Сила тяжести не будет ничем уравновешена. И вещество звезды под действием тяжести начнет падать… падать… падать…

Задача, которую решил Шварцшильд, долго казалась астрономам чисто академической, не имеющей отношения к реальным небесным явлениям, хотя объекты, о которых шла речь у Шварцшильда, и назывались звездами. Больший интерес к этой задаче проявляли физики, но и их в астрономии больше интересовала важная, но чисто физическая проблема источников звездной энергии. Один из пионеров таких исследований – замечательный советский физик Лев Давидович Ландау.

Советский физик Лев Давидович Ландау

Первая заметка Ландау появилась в 1932 году – еще до сообщения об открытии нейтрона. Называлась она “К теории звезд”. Ландау поставил вопрос: какой может быть масса звезды, состоящей из вырожденного ферми-газа? Чандрасекар поставил тот же вопрос раньше и ответил на него. Но Ландау пошел дальше. Он писал: “При М > Мо во всей квантовой теории не существует причины, которая предотвратила бы коллапс системы в точку”.

Именно то, о чем мы только что говорили!

“Звезда будет бесконечно сжиматься!”

В 1937 году Ландау вновь обратился к теории звезд, опубликовав статью “Об источниках звездной энергии”. Нейтроны уже были известны. Нейтронный газ можно сжать значительно сильнее, чем газ из протонов и электронов, ведь нейтроны не заряжены, между ними не действуют силы электрического отталкивания. Естественно был поставлен вопрос: а если?

А если звезда состоит из нейтронов? А если во всех звездах есть нейтронные ядра? А если эти нейтронные ядра и являются источниками звездной энергии? Такие вопросы поставил Ландау в своей статье. На первый из вопросов ответили американские физики Роберт Оппенгеймер и Джордж (Георгий) Майкл Волков через год после того, как прочитали статью советского ученого. Оппенгеймер и Волков первыми решили задачу о том, как может выглядеть нейтронная звезда, какова ее структура.

И помогла им в этом общая теория относительности. Допустим, сказали они, что звезда целиком состоит из нейтронов. В нейтронном газе существует давление вырождения, которое в принципе способно уравновесить поле тяжести. Уравновесить в любой точке звезды. Но чему равна сила тяжести в любой точке звезды? Чтобы рассчитать это, Оппенгеймер и Волков применили общую теорию относительности. И уравновесили тяжесть давлением вырожденного нейтронного газа. Не простого газа, а идеального! В идеальном газе частицы друг с другом не взаимодействуют, и это существенно упрощает вычисления.

Всегда ли давления идеального вырожденного нейтронного газа достаточно для того, чтобы поддержать равновесие звезды? Нет, ответили Оппенгеймер и Волков. Не может существовать нейтронная звезда с массой большей, чем 0,7 массы Солнца. Это меньше предельной массы белого карлика! Впрочем, эта странность не заинтересовала Оппенгеймера с Волковым, как не интересовали их и сами белые карлики – астрофизические проблемы были им чужды.

Как бы то ни было, в 1938 году физики теоретически доказали: да, нейтронные звезды могут существовать. Правда, сами Оппенгеймер и Волков не очень надеялись, что их теоретические расчеты когда-нибудь реализуются в астрономических открытиях. Они писали: “Представляется неправдоподобным, чтобы статические нейтронные ядра играли большую роль в звездной эволюции”. Важность проблемы была таким образом снята, и сама задача стала выглядеть не более чем физическим ребусом.

Но ребус этот не был еще решен окончательно. Что же случится с нейтронной звездой, если масса ее окажется больше найденного предела 0,7 массы Солнца?

Роберт Оппенгеймер (слева) и Джордж Волков (справа)

“Звезда будет бесконечно сжиматься”,-сказали Оппенгеймер и Волков, повторив слово в слово вывод, сделанный ранее Ландау.

Но что стоит за этими словами? За этими словами стояло предсказание черных дыр. О звездах, с поверхности которых не может улететь свет, писали в свое время Мичелл и Лаплас. Но физика черных дыр гораздо богаче! И прежде всего, черная дыра – объект не только невидимый, но принципиально нестационарный. Вот это впервые сказали Оппенгеймер и Волков. А несколько месяцев спустя Оппенгеймер и Снайдер впервые описали, как должна выглядеть черная дыра для нас, наблюдающих с Земли, и для гипотетического космонавта, падающего вместе с веществом звезды к ее центру.

Оказывается, далеко не все равно – откуда смотреть! Одно и то же явление может протекать по-разному, если наблюдать его из различных физических систем отсчета,- так утверждает теория относительности. Время, как вы знаете, сокращается, если двигаться со скоростью, близкой к скорости света. Но если и вы, и космонавт в ракете движетесь равномерно и прямолинейно, то как узнать, кто из вас имеет субсветовую скорость, а кто – черепашью? С вашей точки зрения, летит он, а с его точки зрения, летите вы. С вашей точки зрения, быстрее состариться должны вы, а с его точки зрения – он. Как это проверить?

Вам нужно опять встретиться и сравнить показания часов. Но встретиться-то вы не можете – ведь и вы, и он летите равномерно и прямолинейно в разных направлениях. Чтобы иметь возможность встретиться, кто-то из вас должен развернуться и полететь в обратном направлении. Но тот, кто начнет разворачивать свой корабль, сразу испытает действие ускорения. Тот же, кто летит по-прежнему, никаких ускорений не испытает. А ускорение, согласно принципу эквивалентности, то же самое, что и поле тяжести.

Значит, можно считать, что тот, второй космонавт, вовсе не разворачивал звездолет, включая двигатели, а просто оказался на время в поле тяжести какого-то тела. В поле тяжести – мы уже говорили об этом – часы идут медленнее, даже световые колебания совершаются с меньшей частотой. И чем больше ускорение при развороте (то есть чем больше поле тяжести), тем больше замедление времени. Когда вы снова встретитесь с космонавтом, который улетел и вернулся, окажется, что именно он остался молодым – ведь именно его, а не ваши часы шли медленнее…

“Черные дыры” или “застывшие звезды”?

А теперь вернемся к черной дыре. Представьте, что звезда начала неудержимо сжиматься. Произошел, как говорят астрофизики, катастрофический коллапс, и вы начали падать к центру звезды вместе с ее веществом. Все кругом падает вместе с вами. Вам просто не за что зацепиться взглядом, падает ведь все вещество звезды! И получается, что вы совершенно неподвижны относительно тех частиц вещества, которые летят поблизости от вас и с которыми вы можете сравнивать показания своих часов и длины своих линеек.

Вы неподвижны друг относительно друга даже в момент пересечения сферы Шварцшильда. Для вас при пересечении этой страшной поверхности ничего страшного не произойдет! Вы будете все ускорять свое падение и за доли секунды – по вашим часам – окажетесь в центре звезды вместе со всем ее веществом, которое свалится вам на голову (хотя о какой голове можно говорить, если плотность вещества в центре звезды окажется бесконечно большой).

Наглядная схема того «как устроена» черная дыра

А теперь взглянем на ваше падение с точки зрения астронома, следящего за коллапсом звезды в телескоп. Вот он видит, как в момент, когда газовое давление перестает уравновешивать тяжесть, звезда вдруг начинает быстро уменьшаться в размерах. За полчаса она сжимается (падает…) от размеров Солнца до радиуса нейтронной звезды. Сжатие продолжается, и вы начинаете замечать странности. Вместо того чтобы ускоряться – ведь сила тяжести растет,- падение замедлилось! Да, с приближением к сфере Шварцшильда сила тяжести устремляется к бесконечности.

Но ведь и время начинает течь бесконечно медленно! Если падающая частица сигнализирует о своем движении, ежесекундно испуская по фотону, то вы улавливаете эти фотоны один раз в секунду, один раз в две секунды, один раз в три секунды, в четыре… И при этом энергия фотонов, преодолевших возрастающее поле тяжести, становится все меньше и меньше, пойманные вами фотоны оказываются все “краснее”.

Те фотоны, которые частица излучит вблизи самой сферы Шварцшильда, будут отделены для вас друг от друга интервалами в тысячи, десятки тысяч, миллионы лет. А последний фотон, который частица испустит, пересекая сферу Шварцшильда, дойдет до вас за бесконечное время и будет иметь бесконечно малую энергию. Иными словами, вы этот фотон никогда не увидите.

Что же получилось? Звезда для вас как бы застыла. Процессы, которые вы наблюдаете, протекают все медленнее, пока не застывают окончательно. Впрочем, вряд ли вы вообще сможете что-нибудь наблюдать. Ведь красное смещение света будет так велико, что обычные видимые световые волны станут длинными радиоволнами и будут смещаться все дальше и дальше. Вы увидите, как звезда, начав сжиматься, попросту погасла… Вот какие странные метаморфозы произойдут со звездой, если в ней нечем будет поддерживать равновесие и если начнется катастрофический коллапс.

Так утверждает общая теория относительности. А сами эти звезды получили название коллапсирующих звезд. Впоследствии появилось еще одно название – застывшие звезды. Но укоренилось и стало общепринятым более звучное и экстравагантное название – черные дыры.

Черные дыры, откуда ни один луч света не может выйти к наблюдателю. Черные дыры, которые все заглатывают своим тяготением. Черные дыры, которые, в сущности, не звезды, а растянутый до бесконечности процесс сжатия звезды. Черные дыры, которые и сейчас представляют для теоретиков, для всех знатоков теории относительности увлекательную и не разрешенную пока загадку.

Для сайта starcatalog.ru, компиляция из открытых источников сети интернет, и книги  Павла Рафаэловича Амнуэля, “Загадки для знатоков”