Метод параллакса для измерения расстояния между планетами

Суть метод измерений расстояния между планетами методом параллакса. Точность измерения расстояний методом параллакса.

Что представляет собой метод параллакса

Для определения расстояния до планет можно было использовать явление, называемое параллаксом. Проще всего его можно продемонстрировать так.

• Поставьте перед глазами палец, чтобы он был виден на каком-нибудь пестром фоне.
• Не двигая головой, смотрите на палец по очереди сначала одним глазом, а потом другим.

Вы увидите, что в тот момент, когда вы закрываете один глаз и открываете другой, палец смещается по отношению к фону. Причем ближе вы поднесете палец к глазам, тем больше будет это смещение.

Это происходит потому, что наши глаза расположены на некотором расстоянии друг от друга, так что прямые линии, проведенные от пальца к глазам, образуют заметный угол. Если продолжить эти прямые до фона, они укажут два разных положения пальца. Чем ближе палец к глазам, тем больше этот угол и тем больше кажущееся смещение.

Чтобы измерить расстояние до Луны методом параллакса, достаточно провести наблюдения с двух точек отдаленных друг от друга на сотни километров

Если бы глаза были расставлены шире, это также увеличило бы угол между прямыми, проведенными к пальцу, и палец сместился бы по фону на большее расстояние. Фон обычно так далек, что прямые, проведенные из одной какой-нибудь его точки к глазам, образуют угол, слишком маленький, чтобы его можно было измерить. Поэтому фон можно считать неподвижным.

Тот же самый принцип можно применить и к небесным телам, где “неподвижным фоном” будет звездное небо – звезды находятся слишком далеко и потому кажутся нам с Земли неподвижными.

Как измерить расстояние до Луны методом параллакса

Луна, разумеется, находится так далеко, что при поочередном наблюдении то одним глазом, то другим она нисколько не сместится. Но предположим, что Луну будут одновременно наблюдать на фоне звездного неба астрономы двух обсерваторий, расположенных на расстоянии в несколько сотен километров друг от друга.

Первый наблюдатель будет видеть край Луны па определенном угловом расстоянии от какой-то заранее выбранной звезды, второй же наблюдатель будет видеть в ту же минуту тот же край Луны уже на ином угловом расстоянии от той же звезды.

Если известно смещение Луны по отношению к звездному фону, а также расстояние между обсерваториями, то с помощью несложных тригонометрических формул можно рассчитать расстояние до Луны. Это вполне осуществимо на практике, потому что кажущееся смещение Луны на фоне звезд при изменении позиции наблюдателя достаточно велико.

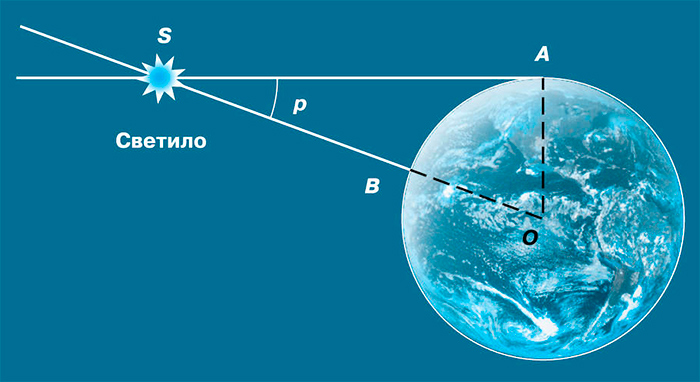
Астрономы путем ряда наблюдений точно установили это смещение для такого положения, когда один наблюдатель видит Луну на горизонте, а другой — прямо над головой. В этом случае основание треугольника равно радиусу Земли, а угол, в вершине которого находится Луна, — это экваториальный горизонтальный параллакс. Его величина оказалась равной 57,04 минуты дуги, или 0,95 градуса дуги.

Это смещение вполне измеримо — оно равно двум видимым диаметрам полной Луны Таким образом, оно может быть определено с достаточной точностью для измерения расстояния до Луны.

Расстояние это, вычисленное с помощью параллакса, хорошо согласовалось с расстоянием, вычисленным с помощью прежнего метода — по земной тени во время лунного затмения.

Измерить расстояние до планет Солнечной системы сложнее методом параллакса – расстояние между точка наблюдения должно измерятся уже тысячами километров

Как измеряются расстояния до планет методом параллакса

К несчастью, планеты Солнечной системы находятся от Земли так далеко, что их смещение на фоне звездного неба при наблюдении из двух обсерваторий слишком мало, чтобы его можно было измерить с достаточной точностью при условиях, существовавших около 1600 г.

Ho в 1608 г. итальянский ученый Галилео Галилей (1564—1642) изобрел телескоп. Телескоп увеличивал не только видимые размеры небесных тел, но и малые смещения, связанные с параллаксом. Таким образом, смещение, слишком малое, чтобы его можно было заметить невооруженным глазом, легко измерялось с помощью телескопа.

В 1671 г. было произведено первое хорошее телескопическое измерение параллакса планеты. Одним из наблюдателей был Жан Рише (1630—1696), французский астроном, возглавлявший научную экспедицию во Французскую Гвиану. Вторым — французский астроном, итальянец по национальности, Джованни Доменико Кассини (1625—1712), остававшийся в Париже.

Одновременно, оба они наблюдали Марс и точно определили его положение относительно соседних звезд. Измерив, насколько различается это положение, и зная расстояние от Кайенны до Парижа, можно было вычислить расстояние до Марса в момент наблюдения.

Как только это расстояние было определено, кеплеровская модель получила масштаб и стало возможно вычислить все остальные расстояния внутри солнечной системы. В частности, Кассини вычислил, что Солнце находится от Земли на расстоянии 140 000 000 км. Это примерно на 10 миллионов километров меньше, чем на самом деле, но для первой попытки результат был превосходным, и его можно считать первым настоящим определением размеров солнечной системы.

На протяжении двух веков после смерти Кассини были произведены более точные измерения параллаксов планет.

В частности, проводились наблюдения над Венерой, когда она проходила между Землей и Солнцем и ее можно было наблюдать в виде крохотного черного пятнышка, движущегося поперек пылающего солнечного диска.

Такие прохождения имели место, например в 1761 и 1769 гг. Если внимательно наблюдать прохождение на разных обсерваториях, то момент, когда Венера коснется солнечного диска, момент, когда она его покинет, и продолжительность прохождения для разных обсерваторий окажутся различными Исходя из этой разницы и из расстояния между обсерваториями, можно вычислить параллакс Венеры, с его помощью — расстояние до нее, а отсюда и расстояние до Солнца.

В 1835 г. немецкий астроном Иоганн Франц Энке (1791—1865), используя данные о прохождении Венеры, вычислил, что расстояние до Солнца равно 152 300 000 км. Это расстояние было больше истинного, но только на 3 000 000 км.

Получить более точные значения было трудно из-за того, что Марс и Венера видны в телескоп как маленькие кружки, а это затрудняло установление точного положения планет. Особенно это касалось Венеры, так как она обладает плотной атмосферой, вызывающей оптические явления, которые мешают определить истинный момент ее соприкосновения с солнечным диском при прохождении.

Наиболее точно установить расстояние до Солнца методом параллакса, удалось только в 1931 году с помощью наблюдения крупных астероидов.

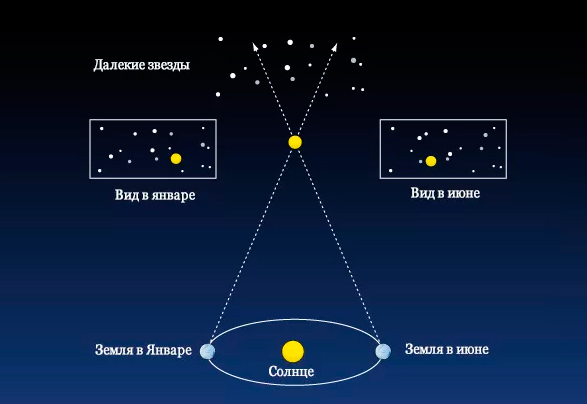
Расстояние до объектов за пределами Солнечной системы, методом параллакса можно измерить с «космических» дистанций – с разных точек орбиты нашей планеты, например

Точность измерения расстояний методом параллакса

В 1898 г. немецкий астроном Карл Густав Витт (1866—1946) открыл Эрос — астероид, орбита которого не лежит целиком в поясе астероидов. Частично она заходит внутрь орбиты Марса и сближается с орбитой Земли.

В 1931 г. Эрос должен был подойти к Земле на расстояние, равное всего лишь ²/₃ наименьшего расстояния до Венеры — ближайшей из больших планет. Такое сближение обещало необычайно большой и легко измеримый параллакс. Кроме того, Эрос настолько мал (25 км в поперечнике), что у него нет атмосферы, которая делала бы его очертания расплывчатыми, и несмотря на свою относительную близость к Земле, он должен был остаться лишь светящейся точкой. Это означало, что его положение можно будет определить с большой точностью.

Были организованы широкие международные наблюдения. Были изучены тысячи фотографий, и в конце концов с помощью параллакса и положения Эроса было установлено, что Солнце находится от Земли на расстоянии, чуть меньшем 149 600 000 км. Это среднее расстояние, так как Земля движется вокруг Солнца не по кругу, а по эллипсу.

При наибольшем сближении с Солнцем (в перигелии) Земля находится от него на расстоянии 146 250 000 км, а при наибольшем удалении (в афелии) — на расстоянии 151 360 000 км.

Несмотря на довольно неплохую точность измерений, метод параллакса пока остается довольно ограниченным в возможностях инструментом из арсенала астрономов. Хотя он вполне годится для относительно точного вычисления расстояний до космических объектов расположенных “в окрестностях” Земли и даже Солнечной системы, с вычислением более далеких расстояний, существуют сложности.

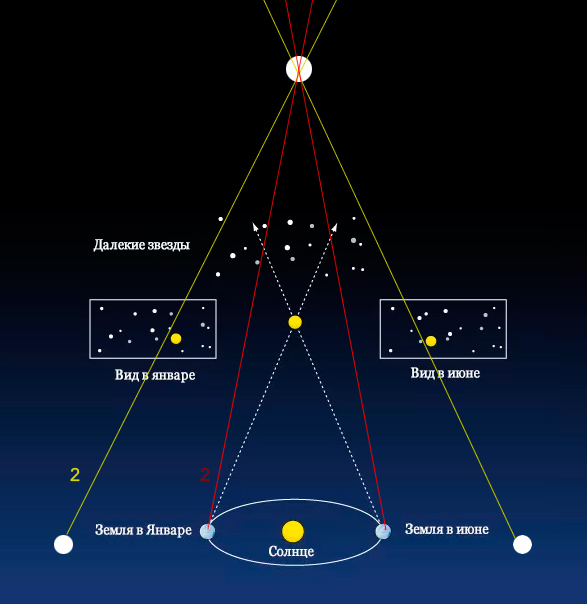
Если пытаться измерить методом параллакса расстояние до очень далекого объекта, точность будет невысокой, и даже диаметра орбиты нашей планеты будет мало для образования подходящего угла. Телескопы придется выносить за пределы орбиты нашей планеты!

Так как для измерения параллакса нужно “взглянуть” на объект с двух максимально удаленных друг от друга точек, то на данный момент мы ограничены в применении этого метода диаметром орбиты Земли – чисто физически мы не можем вынести достаточно мощный телескоп за орбиту нашей планеты, чтобы увеличить угол параллакса и как следствие – прикинуть расстояние до наиболее далеких космических объектов.

Решение этой задачи пока выходит за пределы возможностей техники.